Apa itu zkSNARKs? Panduan Matematika Bulan Seram yang Lengkap

Apa itu zkSNARKs: Spooky Moon Math. Dengan Ethereum memasuki fase Metropolis, itu akan memperkenalkan berbagai perubahan yang akan membuatnya lebih ramah dan ramah privasi. Salah satu perubahan itu adalah pengenalan “Argumen Pengetahuan Non-Interaktif Singkat Pengetahuan Singkat Nol  ” alias Zk-Snarks. Zk-Snarks berjalan pada gagasan nol bukti pengetahuan.

Pada artikel ini, kita akan membahas gagasan nol bukti pengetahuan dan penerapannya dalam teknologi blockchain.

Apa itu zkSNARKs: Spooky Moon Math

Bukti nol Pengetahuan muncul pada 1980-an berkat karya peneliti MIT Shafi Goldwasser, Silvio Micali dan Charles Rackoff. Mereka sedang mengerjakan masalah yang berkaitan dengan sistem bukti interaktif, di mana Prover bertukar pesan dengan Verifier (lebih lanjut tentang prover dan verifier nantinya) untuk meyakinkan mereka bahwa mereka memiliki pengetahuan tentang bukti tertentu tanpa menyatakan apa pengetahuan itu.

Sebelum mereka membuat penemuan tengara, sebagian besar sistem bukti didasarkan pada sifat “sehat” dari sistem bukti. Itu selalu diasumsikan bahwa “pepatah” bisa menjadi jahat dalam setiap skenario di mana mereka akan mencoba menipu pembohong. Ketiga peneliti ini membalikkan gagasan itu dengan mempertanyakan moralitas pemeriksa dan bukan peribahasa. Pertanyaan yang mereka ajukan adalah, bagaimana bisa ada yang tahu dengan pasti bahwa verifier tidak akan membocorkan pengetahuan dan ada juga kekhawatiran tentang jumlah pengetahuan tentang prover bahwa verifier akan mengenal selama proses verifikasi.

Ada berbagai konsekuensi dunia nyata dari teka-teki ini dan salah satu yang paling terkenal berkaitan dengan perlindungan kata sandi.Misalkan Anda ingin masuk ke situs web menggunakan kata sandi.Protokol standar adalah bahwa klien (Anda) akan menulis kata sandi mereka dan mengirimkannya ke server, server kemudian akan meng-hash kata sandi dan menyamakannya dengan hash yang mereka simpan di sistem mereka. Jika nilainya cocok, maka Anda dapat memasuki sistem.

Bisakah Anda melihat cacat besar dalam sistem ini, kan? 

Server memiliki versi plaintext kata sandi Anda, dan privasi Anda berada di tangan server (verifikasi dalam skenario ini). Jika server dikompromikan atau diserang, maka kata sandi Anda akan bersama pihak jahat dan konsekuensinya bisa mengerikan. Untuk menghadapi skenario ini, tidak ada bukti pengetahuan yang benar-benar penting dan pemecahan jalur dalam segala hal.

Ada dua pihak dalam hal nol bukti pengetahuan (sebagaimana dinyatakan di atas), prover dan verifier. Tanpa pengetahuan menyatakan bahwa seorang pepatah dapat membuktikan kepada pemverifikasi bahwa mereka memiliki pengetahuan tertentu tanpa memberi tahu mereka apa sebenarnya pengetahuan itu

Properti bukti pengetahuan nol

Agar ZKP berfungsi, ia harus memenuhi parameter tertentu:

• Kelengkapan: Jika pernyataan itu benar maka pemverifikasi yang jujur ​​dapat diyakinkan oleh pepatah yang jujur.
• Kesehatan: Jika pepatah tidak jujur, mereka tidak dapat meyakinkan verifikasi kebenaran pernyataan dengan berbohong.
• Zero-Knowledge: Jika pernyataan itu benar, pemverifikasi tidak akan tahu apa sebenarnya pernyataan itu.

Jadi sekarang kita memiliki ide dasar tentang apa itu bukti nol-pengetahuan, mari kita periksa beberapa contoh sebelum kita menyelam jauh ke dalam zk-snarks dan penerapannya di blockchain .

Kasus # 1 Gua Alibaba

Dalam contoh ini, pepatah (P) mengatakan kepada pemverifikasi (V) bahwa mereka tahu kata sandi pintu rahasia di bagian belakang gua dan mereka ingin membuktikannya kepada pemverifikasi tanpa benar-benar memberi tahu mereka kata sandi.

Jadi seperti ini tampilannya:

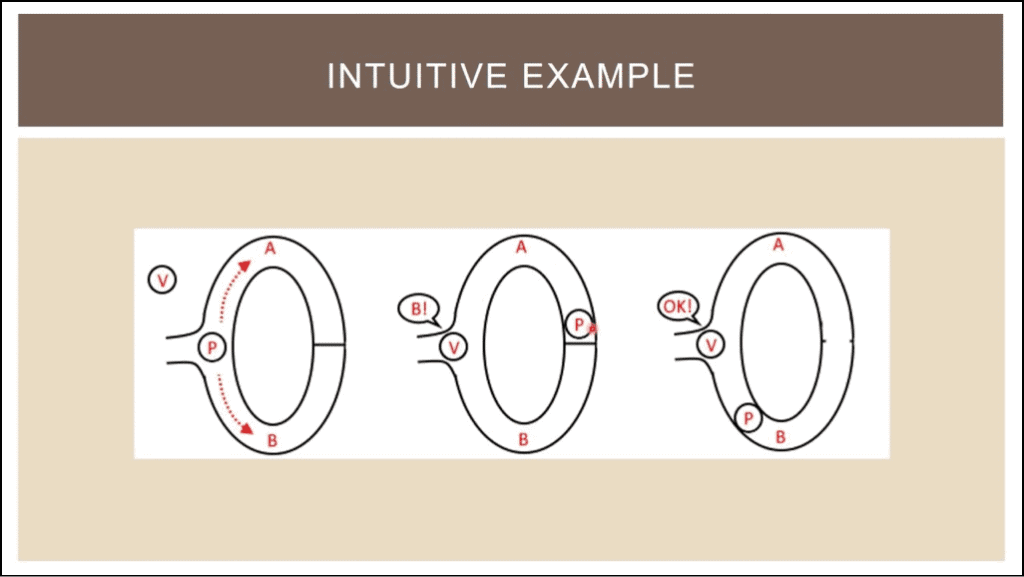
Prover menelusuri salah satu jalur A dan B, misalkan mereka awalnya memutuskan untuk melewati jalur A dan mencapai pintu rahasia di belakang. Ketika mereka melakukannya, verifier V masuk di pintu masuk, tanpa mengetahui jalan mana yang benar-benar diambil oleh prover dan menyatakan bahwa mereka ingin melihat prover muncul dari jalur B.

Dalam diagram, seperti yang Anda lihat, pepatah memang muncul di jalur B. Tapi bagaimana jika ini adalah keberuntungan bodoh?Bagaimana jika pepatah itu tidak tahu kode sandi, dan mengambil jalur B, terjebak di pintu dan oleh keberuntungan belaka, pemeriksa menyuruhnya untuk muncul dari jalur B, yang pada awalnya mereka tempati?

Jadi, untuk menguji validitas, percobaan dilakukan beberapa kali. Jika prover dapat muncul di jalur yang benar setiap saat, itu membuktikan kepada verver bahwa prover memang mengetahui kata sandi meskipun verifier tidak tahu apa kata sandi sebenarnya.

Mari kita lihat bagaimana tiga sifat tanpa pengetahuan terpenuhi dalam contoh ini:

• Kelengkapan: Karena pernyataan itu benar, pepatah yang jujur ​​meyakinkan pemverifikasi yang jujur.
• Kelancaran: Jika pepatah tidak jujur, mereka tidak dapat membodohi pemverifikasi karena tes dilakukan beberapa kali. Akhirnya, keberuntungan pepatah harus habis.
• Zero-Knowledge: Verifier tidak pernah tahu apa kata sandinya, tetapi yakin bahwa pemiliknya memilikinya.

Kasus # 2 Menemukan Waldo

Ingat menemukan Waldo?

Tentu saja, Anda harus melihatnya di suatu tempat, baik dalam kehidupan nyata maupun online. Bagi mereka yang tidak tahu, Finding Waldo adalah permainan di mana Anda harus menemukan “Waldo” di antara lautan orang. Ini adalah game “Spot the guy” yang sederhana. Hanya untuk memberi Anda ide dasar, seperti inilah bentuk gim ini:

Dan idenya adalah menemukan Waldo yang terlihat seperti ini:

Sepertinya cukup mudah bukan? Temukan orang ini di antara lautan orang lain yang Anda lihat dalam permainan. Ok, jadi dari mana konsep Zero Knowledge muncul di sini? Bayangkan ada dua orang Anna dan Carl. Anna memberi tahu Carl bahwa dia tahu di mana Wally berada tetapi dia tidak ingin menunjukkan di mana tepatnya dia. Jadi, bagaimana dia bisa membuktikan kepadanya bahwa dia telah menemukan Wally tanpa menunjukkan posisi yang tepat?

Ada, sebuah makalah yang menarik oleh Naor, Naor dan Reingold yang menunjukkan dua solusi Zero Knowledge untuk masalah ini.Ada “Solusi Berteknologi Menengah” dan “Solusi Berteknologi Rendah”. Mari kita bahas keduanya.

Solusi Mid-Tech

Alasan mengapa solusi ini adalah “teknologi menengah” adalah karena prover dan verifier kami memerlukan akses ke mesin fotokopi untuk membuat pekerjaan ini. Jadi begini caranya. Pertama, Anna dan Carl akan membuat fotokopi dari game aslinya. Kemudian Anna, sambil memastikan bahwa Carl tidak melihat, akan memotong Waldo dari fotokopi dan kemudian menghancurkan sisanya. Setelah itu dia dapat menunjukkan Waldo cocok untuk Carl dan membuktikan bahwa dia tahu di mana Waldo setelah semua tanpa menunjukkan lokasi tepatnya ke Carl.

Ada masalah dengan solusi ini. Meskipun memenuhi kriteria “Nol Pengetahuan”, itu tidak memenuhi kriteria “Kesehatan”. Ada banyak cara yang bisa dilakukan Anna untuk menipu di sini. Dia bisa saja memotong secara acak Waldo sejak awal dan bisa menunjukkannya pada Carl tanpa benar-benar tahu di mana Waldo berada. Jadi apa solusinya?

Solusi untuk ini adalah pengujian yang teliti dan cermat. Pertama, Anna dan Carl akan mengambil fotokopi permainan. Kemudian Carl akan menggambar pola khas di bagian belakang fotokopi. Setelah itu, Carl akan mengantar Anna ke sebuah ruangan di mana dia akan diisolasi dan tidak memiliki kesempatan untuk menipu apa pun. Jika Anna keluar dengan potongan Waldo, maka Carl dapat diyakinkan bahwa dia benar-benar tahu di mana Waldo tanpa mengungkapkan solusinya. Mereka dapat mengulangi percobaan ini beberapa kali dan Carl dapat membandingkan guntingan berbeda dari Waldo untuk lebih yakin tentang validitas klaim Anna.

Solusi Berteknologi Rendah

Solusi ini membutuhkan peralatan yang sangat mendasar. Idenya sederhana. Dapatkan karton besar, yang berukuran dua kali lipat dari gim dan potong persegi panjang kecil di atasnya. Sekarang, ketika Carl tidak melihat, Anna dapat memindahkan kardus pada permainan sedemikian rupa sehingga persegi panjang langsung di atas Waldo.Sekarang, dia dapat memberi tahu Carl untuk melihat dan inilah yang akan dilihatnya:

Jadi, sementara Carl mungkin mendapatkan ide yang sangat mendasar tentang di mana sebenarnya Waldo berada, dia tidak tahu lokasi yang tepat. Karenanya Anna telah membuktikan kepada Carl bahwa dia tahu di mana Waldo tanpa menentukan lokasi pastinya.

Kasus # 3: Sudoku

Aplikasi hebat tanpa pengetahuan lainnya adalah di Sudoku. Bagi mereka yang tidak tahu, Sudoku adalah teka-teki Jepang di mana Anda mendapatkan meja 9X9 yang terlihat seperti ini:

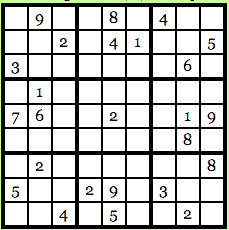
Idenya adalah untuk mengisi setiap baris, setiap kolom dan setiap blok 3X3 dengan angka 1-9 dan tidak ada angka yang harus diulang.Jadi, solusi untuk teka-teki di atas terlihat seperti ini:

Seperti yang Anda lihat, setiap baris, kolom, dan blok 3X3 unik dan tidak ada satu nomor pun yang diulang. Mari kita kembali ke teman lama kita Anna dan Carl. Anna telah menemukan solusi untuk teka-teki Sudoku dan Carl, skeptis bahwa dia tidak percaya padanya dan ingin Anna membuktikan bahwa dia memang tahu solusinya. Anna ingin membuktikan kejujurannya, tetapi pada saat yang sama, dia tidak ingin Carl tahu solusi pasti dari teka-teki itu. Bagaimana dia melakukannya? Anna akan menggunakan Zero Knowledge untuk membuktikan validitas klaimnya.

Pertama, Carl akan menjalankan solusi Sudoku melalui program komputer yang telah diverifikasi, jujur ​​dan program akan menjalankan angka-angka melalui cipher substitusi yang dipilih secara acak. Katakan, untuk masalah khusus ini, sandi yang dipilih oleh program adalah ini:

Program dan sandi yang dipilih sedemikian rupa sehingga setiap digit memiliki peluang yang sama untuk ditransmisikan ke dalam substitusi seperti halnya angka lainnya. Pada dasarnya, 1 memiliki peluang yang sama untuk ditransmisikan seperti halnya 3 dan 4 memiliki peluang yang sama untuk ditransmutasikan seperti 9 dan seterusnya dan seterusnya. Jadi, menggunakan sandi ini memberi kita solusi berikut untuk teka-teki di atas:

Anna mendapatkan solusi yang ditransmisikan sekarang, perlu diingat bahwa Carl masih tidak tahu apa solusi aslinya dan dia juga tidak memiliki solusi yang ditransmisikan. Jadi, yang dilakukan Anna sekarang adalah dia menyembunyikan semua angka dalam teka-teki dengan menggunakan “mekanisme kotak kunci”, pada dasarnya Carl tidak akan dapat melihat angka-angka itu dan akan melihat kisi kosong 9X9 di depannya.

Carl sekarang memiliki 28 pilihan di depannya:

• Ungkapkan satu baris.
• Buka kolom.
• Buka kotak 3X3.
• Mengungkapkan versi transmutasi dari teka-teki asli.

Misalkan Carl ingin tahu seperti apa baris ketiga:

Ini yang akan dia lihat. Carl akan melihat bahwa setiap angka di baris itu unik dan karena setiap angka yang mungkin dalam solusi asli memiliki probabilitas yang sama untuk ditransmisikan melalui cipher, Carl tidak akan tahu apa solusi aslinya.

Sekarang anggaplah, Carl memutuskan untuk mengambil opsi terakhir dan ingin melihat seperti apa puzzle aslinya ketika ditransmisikan:

Sekali lagi, karena sandi dipilih secara acak dan semua angka memiliki probabilitas yang sama untuk ditransmisikan, Carl tidak akan tahu apa solusi aslinya. Carl sekarang bisa melalui semua 28 pilihannya dan akhirnya dia akan puas dengan validitas pernyataan Anna.

Mengapa?

Karena, jika Anna memang selingkuh, tidak mungkin dia bisa menemukan sandi untuk memberikan solusi unik untuk semua 28 pilihan Carl. Jika Carl hanya memilih satu opsi, peluang Anna lolos dari kecurangan adalah 27/28. TETAPI jika Carl memilih untuk melakukan tes acak beberapa kali, misalkan dia memilih untuk mengujinya 150 kali, pilihan Anna untuk lolos dengan kecurangan turun ke (27/28) ^ 150 yang <0,5%.

Jadi, mari kita periksa nol properti pengetahuan dari skenario ini:

• Kelengkapan: Program sandi yang digunakan telah diverifikasi, jujur, dan Anna dan Carl mengikuti protokol.
• Kesehatan: Jika Carl melakukan tes acak 150 kali, peluang Anna lolos dari kecurangan adalah <0,5%.
• Zero-Knowledge: Anna tidak pernah mengungkapkan kepada Carl apa solusi aslinya.

Bukti vs Bukti Pernyataan

Sekarang setelah kita mengetahui aspek teoritis dari nol bukti pengetahuan dan penerapannya dalam berbagai contoh, apa penerapan praktisnya dalam blockchain? Mengapa semua orang mengoceh tentang Zcash untuk menerapkan ZKP (tanpa bukti pengetahuan) dan mengapa semua orang senang dengan Ethereum melakukan hal yang sama? Sebelum kita membahasnya, penting untuk mengetahui satu lagi konsep teoretis yang penting.

Apa sebenarnya yang kita buktikan dengan menggunakan ZKP?Dalam spektrum luas, ada dua pernyataan yang bisa Anda buktikan dengan menggunakan ZKP. Bukti alias fakta dan bukti pengetahuan.

• Bukti: Ini adalah kebenaran intrinsik tentang alam semesta yang mungkin ingin Anda buktikan melalui ZKP. Misalnya. “Nomor X milik grup Y”.

• Bukti pengetahuan: Anda mungkin juga ingin membuktikan bahwa Anda memiliki pengetahuan tentang ide tertentu tanpa mengungkapkan apa itu pengetahuan tertentu. Seperti dapat dilihat pada contoh gua Sudoku, Waldo dan Alibaba yang diberikan di atas.

Penting untuk dicatat perbedaan antara keduanya karena mereka sama sekali berbeda. Dalam dunia cryptocurrency, kita sebagian besar fokus pada “bukti pengetahuan”. Salah satu terobosan paling penting dalam membuktikan bukti pengetahuan melalui nol bukti pengetahuan datang ketika Claus-Peter Schnorr pada 1980-an muncul dengan protokol identifikasi Schnorr. Protokol ini memberikan dasar-dasar kriptografi tanda tangan kunci modern dan menampilkan bagaimana Zero-knowledge dapat diintegrasikan dengan mulus ke dalam praktik kriptografi modern.

Protokol Identifikasi Schnorr

Untuk memahami apa itu Identifikasi Schnorr, mari kita bawa kembali teman lama kita Anna dan Carl. Anna telah mengumumkan kepada dunia bahwa dia memiliki kunci publik dan dapat menerima dan menerima informasi melalui itu. Carl, yang selalu skeptis, berpikir bahwa Anna berbohong. Satu-satunya cara Anna dapat membuktikan kejujurannya adalah dengan menunjukkan kunci pribadinya kepada Carl, tetapi ia tidak ingin mengungkapkan kunci pribadinya.

Jadi, bagaimana Anna akan mengungkapkan pengetahuannya tentang kunci pribadinya tanpa mengungkapkannya? Di sinilah protokol Schnorr masuk. Bahkan sebelum kita mulai memahami cara kerja protokol, ada beberapa parameter yang perlu Anda ketahui:

• p = Semua bilangan prima.
• q = faktor p-1.
• “A” sedemikian rupa sehingga a ^ q = 1 mod hlm.

Sekarang perlu diingat, dalam protokol Schnorr, 3 variabel ini bersifat global. Berarti siapa pun memiliki pengetahuan tentang apa 3 variabel ini untuk skenario tertentu.

Sekarang kita sampai pada dua kunci, kunci privat rahasia yang akan kita sebut “s” dan kunci publik yang akan kita sebut “v”.

s dapat berupa nilai apa saja selama 0 <s <q.

v = a ^ -s mod q.

Kunci publik “v” akan menjadi pengetahuan global dan publik bersama dengan p, q dan a. Namun, HANYA Anna akan memiliki pengetahuan tentang “s” itu, karena itu adalah kunci pribadinya.

Jadi, sekarang kita telah mendefinisikan variabel, mari kita lihat bagaimana pertukaran informasi dan validitas pernyataan Anna dapat bekerja TANPA dia mengungkapkan apa kunci privat itu.

Anna menandatangani dan mengirim pesan terenkripsi

Misalkan Anna ingin mengirim pesan “M” ke Carl yang dikodekan dengan kunci pribadinya. Bagaimana dia akan melakukannya jika dia mengikuti protokol Schnorr?

Pertama, dia akan memilih angka acak “r” sehingga 0 <r <q.

Sekarang dia akan menghitung nilai x sedemikian rupa sehingga:

X = a ^ r mod p.

Sekarang dia telah menghitung nilai X, dia akan menyatukan ini dengan pesan aslinya. Apa itu penggabungan? Misalkan kita memiliki dua string “halo” dan “dunia”. Jika kita menggabungkan keduanya, maka kita akan mendapatkan “hello world”. Penggabungan pada dasarnya berarti menambahkan dua string dan menjadikannya satu.

Jadi, dia akan menggabungkan M dan X untuk mendapatkan M || X.dan dia akan menyimpan hash dari nilai ini di e.

Pada dasarnya, e = H (M || X) di mana H () adalah fungsi hash.

Akhirnya, ketika semua ini dilakukan, dia akan melakukan satu perhitungan terakhir. Dia akan mendapatkan nilai “y” sehingga:

y = (r + s * e) mod q

Sekarang setelah semua perhitungan selesai, dia akan mengirim informasi berikut ini ke Carl:

• Pesan “M”.
• Tanda tangan e dan y.

Carl menerima pesan dan memverifikasi bukti pengetahuan Anna

Sekarang Carl telah menerima informasi berikut dari Anna: Pesan (M) dan tanda tangan (e dan y).

Bersamaan dengan itu, ia memiliki informasi berikut yang diketahui publik untuk semua orang:

• Kunci publik Anna “v”.
• Bilangan prima yang dipilih Anna “p”.
• “Q” yang merupakan faktor “p-1” yang dipilih Anna.
• Dan “a” sehingga a ^ q = 1 mod p, ini juga Anna pilih.

Sekarang, Carl harus menghitung X ‘sedemikian rupa sehingga:

X ‘= a ^ y * v ^ e mod hlm.

Sekarang mari kita lakukan substitusi sederhana:

Kita tahu bahwa v = a ^ -s, mari gantikan itu dalam persamaan di atas dan kita dapatkan:

• X ‘= a ^ y * a ^ -se = a ^ (ys * e).
• Sekarang kita juga tahu bahwa y = r + s * e.
• Yang berarti: r = ys * e.

Mari gantikan nilai ini dalam persamaan di atas:

• Kami mendapatkan: X ‘= a ^ r.
• Seperti yang telah kita lihat di atas: X = a ^ r.
• Jadi secara teknis: X = X ‘.

Tetapi Carl tidak tahu nilai “X” karena dia tidak pernah menerima nilai itu. Semua yang dia terima adalah sebagai berikut: Pesan M, tanda tangan (e dan y) dan sejumlah variabel publik (kunci publik “v”, p, q, dan a).

Dia tidak pernah menerima “X” tetapi dia tahu bahwa jika Anna berbicara kebenaran maka X ‘harus sama dengan X.

Tapi, dia tahu nilai e dan pesan M.

Jadi dia akan memecahkan untuk e dengan melakukan hal berikut:

e = H (M || X ‘).

Perhatikan bahwa sebelumnya kita memecahkan e dengan melakukan: H (M || X).

Jadi, dengan logika itu, jika dua nilai e muncul sama maka itu berarti X = X ‘.

Ini juga berarti bahwa Anna memang memiliki kunci pribadi selama ini dan dia tidak berbohong.

Jadi, mari kita jalankan seluruh skenario ini melalui tiga properti tanpa bukti pengetahuan:

• Kelengkapan: Carl yakin akan kejujuran Anna karena pada akhirnya X = X ‘.
• Kesehatan : Rencana itu baik karena satu-satunya cara Anna dapat membuktikan kejujurannya adalah dengan menggunakan kunci pribadinya. Dia tidak mungkin berbohong tentang memiliki kunci pribadi.
• Tanpa Pengetahuan: Carl tidak pernah menemukan apa kunci privat Anna.

Protokol Schnorr memberikan aplikasi kriptografis dunia nyata dari nol bukti pengetahuan.

Bagaimana membuat nol bukti pengetahuan menjadi non-interaktif?

Dengan sistem verifikasi tanpa pengetahuan sebelumnya, ada satu masalah besar. Agar berfungsi, prover dan verifier harus online pada saat yang sama. Dengan kata lain, prosesnya adalah “interaktif”. Ini membuat seluruh sistem tidak efisien dan hampir tidak mungkin untuk ditingkatkan. Verifier tidak mungkin online saat bersamaan dengan prover? Perlu ada sistem untuk membuatnya lebih efisien.

Pada tahun 1986, Fiat dan Shamir menemukan heuristik Fiat-Shamir dan berhasil mengubah bukti nol-pengetahuan interaktif menjadi bukti nol pengetahuan non-interaktif. Ini membantu seluruh protokol bekerja tanpa interaksi apa pun. Prosedur di belakangnya sangat sederhana.

Jadi, untuk memberi Anda contoh, ini adalah bagaimana nol bukti pengetahuan yang digunakan untuk bekerja sebelum Fiat dan Shamir.

Mari kita buktikan ini menggunakan logaritma diskrit sederhana.

• Anna ingin membuktikan kepada Carl bahwa dia tahu nilai x sedemikian rupa sehingga y = g ^ x ke basis g.

• Anna mengambil nilai acak v dari sekumpulan nilai Z, dan menghitung t = g ^ v dan mengirimkan t ke Carl.

• Carl mengambil nilai acak c dari set Z dan mengirimkannya ke Anna.

• Anna menghitung r = vc * x dan mengembalikan r ke Carl.

• Carl memeriksa apakah t = g ^ r * y ^ c tahan atau tidak (karena r = vc * x, y = g ^ x dan dengan substitusi sederhana, g ^ (vc * x) * g ^ c * x = g ^ v = t).

• Carl tidak tahu nilai x, hanya dengan memeriksa apakah t = g ^ r * y ^ c ia dapat memverifikasi bahwa Anna memang tahu nilai x.

Sekarang sementara interaksi di atas adalah nol-pengetahuan, masalah dengan ini adalah bahwa Anna dan Carl harus online dan bertukar nilai agar bisa berfungsi.

Bagaimana Anna dapat membuktikan kepada Carl bahwa ia memiliki pengetahuan tentang sesuatu tanpa Carl online? Dia dapat melakukannya dengan menggunakan fungsi hash kriptografi sederhana, seperti Fiat dan Shamir berteori.

Mari kita lihat bagaimana contoh di atas bekerja dengan cara yang tidak interaktif:

• Anna ingin membuktikan kepada Carl bahwa dia tahu nilai x sedemikian rupa sehingga y = g ^ x ke basis g.

• Anna mengambil nilai acak v dari sekumpulan nilai Z, dan menghitung t = g ^ v.

• Anna menghitung c = H (g, y, t) di mana H () adalah fungsi hash.

• Anna menghitung r = v – c * x.

• Carl atau siapa pun dapat memeriksa apakah t = g ^ r * y ^ c.

Jadi, seperti yang Anda lihat, nol bukti pengetahuan dibuat non-aktif.Dan inilah yang meletakkan dasar bagi Zk-Snarks.

Apa gunanya Zk-Snarks?

Zk-Snarks singkatan dari “Argumen Pengetahuan Non-Interaktif Ringkas Tanpa Pengetahuan Nol”. Penggunaannya dalam teknologi blockchain modern sangat besar. Untuk memahami penerapannya, penting untuk mengetahui cara kerja kontrak cerdas. Kontrak pintarpada dasarnya adalah escrow dana yang diaktifkan setelah fungsi tertentu selesai.

Misalnya. Anna menempatkan 100 ETH dalam kontrak pintar yang dia dapatkan dengan Carl. Carl harus melakukan tugas tertentu, yang penyelesaiannya, Carl akan mendapatkan 100 ETH dari kontrak pintar.

Ini menjadi rumit ketika tugas-tugas yang harus dilakukan Carl adalah berlapis-lapis dan rahasia. Misalkan Anda telah memasukkan kontrak pintar dengan Anna. Sekarang, Anda hanya akan mendapatkan pembayaran jika Anda melakukan A, B, dan C. Bagaimana jika Anda tidak ingin mengungkapkan rincian A, B, dan C karena itu rahasia untuk perusahaan Anda dan Anda tidak ingin ada pesaing tahu apa yang harus kamu lakukan?

Apa yang dilakukan Zk-Snarks adalah membuktikan bahwa langkah-langkah tersebut telah diambil dalam kontrak pintar tanpa mengungkapkan apa langkah-langkah itu sebenarnya. Hal yang sangat berguna adalah melindungi Anda dan privasi perusahaan Anda. Itu hanya dapat mengungkapkan bagian dari proses tanpa menunjukkan keseluruhan proses itu sendiri dan membuktikan bahwa Anda jujur ​​tentang klaim Anda.

Bagaimana cara kerja ZkSnarks?

Zk-Snark terdiri dari 3 algoritma: G, P dan V.

G adalah generator kunci yang mengambil input “lambda” (yang harus dijaga kerahasiaannya dan tidak boleh diungkapkan dalam keadaan apa pun) dan program C. Kemudian dihasilkan untuk menghasilkan dua kunci yang tersedia untuk umum, pk kunci yang membuktikan, dan verifikasi kunci vk. Kunci-kunci ini bersifat publik dan tersedia untuk salah satu pihak terkait.

P adalah prover yang akan menggunakan 3 item sebagai input. Pk kunci pembuktian, input acak x, yang tersedia untuk umum, dan pernyataan pribadi bahwa mereka ingin membuktikan pengetahuan tanpa mengungkapkan apa sebenarnya. Sebut saja pernyataan pribadi itu “w”. Algoritma P menghasilkan prf bukti sedemikian rupa sehingga: prf = P (pk, x, w).

Algoritma verifier V pada dasarnya mengembalikan variabel boolean.Variabel Boolean hanya memiliki dua pilihan, bisa BENAR atau bisa SALAH. Jadi, verifier mengambil kunci verifikasi, input publik x dan bukti prf sebagai input seperti:

V (vk, x, prf)

..dan mengembalikan TRUE jika prover benar dan salah sebaliknya.

Sekarang, tentang parameter lambda. Nilai “Lambda” harus dirahasiakan karena siapa pun dapat menggunakannya untuk menghasilkan bukti palsu. Bukti palsu ini akan mengembalikan nilai BENAR terlepas dari apakah pepatah benar-benar memiliki pengetahuan tentang pernyataan pribadi “w” atau tidak.

Fungsionalitas ZkSnarks

Untuk memperlihatkan fungsionalitas Zk-Snark, kita akan menggunakan fungsi contoh yang sama dengan yang digunakan Christian Lundkvist dalam artikelnya untuk Consensys. Seperti inilah contoh programnya:

fungsi C (x, w)

{

return (sha256 (w) == x);

}

Pada dasarnya, fungsi C mengambil 2 nilai sebagai input, nilai hash publik “x” dan pernyataan rahasia yang perlu diverifikasi “w”. Jika nilai hash SHA-256 dari w sama dengan “x” maka fungsi mengembalikan TRUE jika tidak mengembalikan FALSE. (SHA-256 adalah fungsi hash yang digunakan dalam Bitcoin).

Mari kita bawa kembali teman lama kita Anna dan Carl untuk contoh ini. Anna menjadi pepatah dan Carl yang skeptis adalah pembuktinya.

Hal pertama yang harus dilakukan Carl, sebagai pemverifikasi, adalah membuat kunci pembuktian dan verifikasi menggunakan generator G. Untuk ini, Carl perlu menghasilkan nilai acak “lambda”. Seperti yang dinyatakan di atas, bagaimanapun, dia harus sangat berhati-hati dengan Lambda karena dia tidak bisa membiarkan Anna tahu nilainya untuk menghentikannya dari membuat bukti palsu.

Bagaimanapun, ini akan terlihat seperti:

G (C, lambda) = (pk, vk).

Sekarang setelah dua kunci dibuat, Anna perlu membuktikan validitas pernyataan dengan membuat bukti. Dia akan menghasilkan bukti menggunakan algoritma pembuktian P. Dia akan membuktikan bahwa dia tahu nilai rahasia “w” yang hashes (pada parsing melalui SHA-256) untuk memberikan output x. Jadi, algoritma pembuktian untuk pembuatan bukti terlihat seperti ini:

prf = P (pk, x, w).

Sekarang dia telah menghasilkan bukti “prf”, dia akan memberikan nilai kepada Carl yang akhirnya akan menjalankan algoritma verifikasi Zk-Snarks.

Ini akan terlihat seperti apa:

V (vk, x, prf).

Di sini, vk adalah kunci verifikasi dan x adalah nilai hash yang diketahui dan prf adalah bukti bahwa ia mendapatkan dari Anna. Jika algoritma ini mengembalikan TRUE maka ini berarti Anna jujur ​​dan dia memang memiliki nilai rahasia “w”. Jika mengembalikan FALSE maka ini berarti Anna berbohong tentang mengetahui “w”.

Penggunaan ZkSnarks dalam cryptocurrency

Zcash adalah cryptocurrency diluncurkan oleh Zerocoin Electic Coin Perusahaan pada 9 th September 2016 dan merupakan contoh pertama cryptocurrency menikah konsep teknologi blockchain dengan ZkSnarks. Ini bertujuan untuk memberikan ruang transaksi yang sepenuhnya aman dan terlindung bagi penggunanya tanpa mengungkapkan detail (seperti alamat mereka) kepada siapa pun.

Ethereum ingin mengintegrasikan ZkSnarks saat memasuki fase Metropolis dan cara mereka berencana untuk melakukannya adalah dengan menciptakan aliansi dengan Zcash yang akan mencakup pertukaran nilai yang saling menguntungkan. Kepala pengembangZcash, Zooko Wilcox, memberikan presentasi di DevCon2 di Shanghai yang mengeksplorasi masa depan aliansi semacam itu. Menurutnya, ada 3 cara Z-Cash dan dengan ekstensi, zk-snarks dapat diintegrasikan dengan Ethereum.

Metode pertama disebut BaZoe (Zoe = Zcash on Ethereum). Ia menambahkan pra-kompiler zk-snark di Ethereum dan membuatkontrak pintar Zcash mini di Ethereum. Idenya adalah untuk melihat apakah sistem Ethereum dapat membuat DAPP yang diaktifkan zk-snark di atas blockchain -nya .

Metode kedua adalah untuk mengintegrasikan komputasi Ethereum di dalam blockchain Zcash . Seperti yang dikatakan Wilcox, aset terbesar Ethereum adalah kemampuan komputasinya dan orang ingin melihat apakah mereka dapat mengintegrasikannya pada blockchain berbasis zk-snark seperti Zcash. Bisakah orang membuat DAPPS pada blockchain yang dibuat tanpa bukti pengetahuan? Itu adalah sesuatu yang mereka tunggu untuk lihat.

Aspek ketiga dan yang paling menarik adalah Project Alchemy. Ini pada dasarnya adalah koneksi dan interoperasi dari kedua blockchain sehingga seseorang dapat bergerak mulus di antara keduanya. Cara yang Zcash rencanakan untuk melakukannya adalah dengan mengklon BTC Relay. Ini adalah skrip Ethereum yang ditulis untuk membuat klien cahaya Bitcoin di dalam Ethereum. The Zcash clone akan menggunakan konsep yang sama untuk membuat Zcash klien cahaya di dalam Ethereum.

Jika ini berhasil maka kita akan memiliki sistem mata uang terdesentralisasi pertama di dunia yang memfasilitasi pembuatan DAPPS tanpa pengetahuan yang tertanam di dalamnya.

Melihat ke depan

Tidak ada keraguan bahwa pengenalan zero knowledge proofs akan menjadi game changer yang sangat besar untuk Ethereum . Dalam dunia yang semakin terbuka, terhubung, dan diawasi, segala jenis privasi diterima. Bagaimana integrasi terjadi masih harus dilihat, tetapi dengan konsep-konsep teoretis itu sendiri, orang tidak bisa tidak bersemangat.

-AMAZONPOLLY-ONLYAUDIO-MULAI-Apa itu zkSNARKs: Spooky Moon Math. Dengan Ethereum memasuki fase Metropolis, itu akan memperkenalkan berbagai perubahan yang akan membuatnya lebih ramah dan ramah privasi. Salah satu perubahan itu adalah pengenalan “Argumen Pengetahuan Non-Interaktif Singkat Pengetahuan Singkat Nol” alias Zk-Snarks. Zk-Snarks berjalan pada gagasan nol bukti pengetahuan. Pada artikel ini, kita akan membahas gagasan nol bukti pengetahuan dan penerapannya dalam teknologi blockchain. Apa itu zkSNARKs: Spooky Moon Math Zero Bukti pengetahuan muncul pada tahun 1980-an berkat karya peneliti MIT Shafi Goldwasser, Silvio Micali dan Charles Rackoff. Mereka sedang mengerjakan masalah yang terkait dengan sistem bukti interaktif, di mana Prover bertukar pesan dengan Verifier (lebih lanjut tentang prover dan verifikator nanti) untuk meyakinkan mereka bahwa mereka memiliki pengetahuan tentang bukti tertentu tanpa menyatakan apa pengetahuan itu. Sebelum mereka membuat penemuan tengara, sebagian besar sistem bukti didasarkan pada sifat “sehat” dari sistem bukti. Itu selalu diasumsikan bahwa “pepatah” bisa menjadi jahat dalam setiap skenario di mana mereka akan mencoba menipu pembohong. Ketiga peneliti ini membalikkan gagasan itu dengan mempertanyakan moralitas pemeriksa dan bukan peribahasa. Pertanyaan yang mereka ajukan adalah, bagaimana bisa ada yang tahu dengan pasti bahwa verifier tidak akan membocorkan pengetahuan dan ada juga kekhawatiran tentang jumlah pengetahuan tentang prover bahwa verifier akan mengenal selama proses verifikasi. Mulai Uji Coba Gratis Anda Hari Ini Uji Coba Gratis Ada berbagai konsekuensi dunia nyata dari teka-teki ini dan salah satu yang paling terkenal berkaitan dengan perlindungan kata sandi. Misalkan Anda ingin masuk ke situs web menggunakan kata sandi. Protokol standar adalah bahwa klien (Anda) akan menulis kata sandi mereka dan mengirimkannya ke server, server kemudian akan meng-hash kata sandi dan menyamakannya dengan hash yang mereka simpan di sistem mereka. Jika nilainya cocok, maka Anda dapat memasuki sistem. Bisakah Anda melihat cacat besar dalam sistem ini, kan? Server memiliki versi plaintext kata sandi Anda, dan privasi Anda berada di tangan server (verifikasi dalam skenario ini). Jika server dikompromikan atau diserang, maka kata sandi Anda akan bersama pihak jahat dan konsekuensinya bisa mengerikan. Untuk mengatasi skenario ini, bukti nol pengetahuan sangat penting dan jalur melanggar dalam segala hal. Ada dua pihak dalam hal nol bukti pengetahuan (sebagaimana dinyatakan di atas), prover dan verifier. Nol pengetahuan menyatakan bahwa seorang pepatah dapat membuktikan kepada pemverifikasi bahwa mereka memiliki pengetahuan tertentu tanpa memberi tahu mereka apa sebenarnya pengetahuan itu. Sifat-sifat bukti nol pengetahuan Agar ZKP dapat berfungsi, perlu memenuhi parameter tertentu: Kelengkapan: Jika pernyataan itu benar maka verifier yang jujur ​​dapat diyakinkan oleh pepatah yang jujur. Kesehatan: Jika pepatah tidak jujur, mereka tidak dapat meyakinkan verifikasi kebenaran pernyataan dengan berbohong. Zero-Knowledge: Jika pernyataan itu benar, pemverifikasi tidak akan tahu apa sebenarnya pernyataan itu. Jadi sekarang kita memiliki ide dasar tentang apa bukti tanpa pengetahuan itu, mari kita lihat beberapa contoh sebelum kita menyelam lebih dalam ke zk-snarks dan aplikasinya di blockchain. Kasus # 1 Gua Alibaba Dalam contoh ini, pepatah (P) mengatakan kepada pemverifikasi (V) bahwa mereka tahu kata sandi pintu rahasia di bagian belakang gua dan mereka ingin membuktikannya ke pemverifikasi tanpa benar-benar memberi tahu mereka kata sandi. Jadi seperti inilah tampilannya: Gambar milik: Scott Twombly (saluran YouTube) The Prover menyusuri salah satu jalur A dan B, misalkan mereka awalnya memutuskan untuk melewati jalur A dan mencapai pintu rahasia di belakang. Ketika mereka melakukannya, verifier V masuk di pintu masuk, tanpa mengetahui jalan mana yang benar-benar diambil oleh prover dan menyatakan bahwa mereka ingin melihat prover muncul dari jalur B. Dalam diagram, seperti yang Anda lihat, prover tidak memang muncul di jalur B. Tetapi bagaimana jika ini adalah keberuntungan yang bodoh? Bagaimana jika pepatah itu tidak tahu kode sandi, dan mengambil jalur B, terjebak di pintu dan oleh keberuntungan belaka, pemeriksa menyuruhnya untuk muncul dari jalur B, yang pada awalnya mereka tempati? Jadi, untuk menguji validitas, percobaan dilakukan beberapa kali. Jika prover dapat muncul di jalur yang benar setiap saat, itu membuktikan kepada verver bahwa prover memang mengetahui kata sandi meskipun verifier tidak tahu apa kata sandi sebenarnya. Mari kita lihat bagaimana tiga sifat dari nol pengetahuan terpenuhi dalam contoh ini: Kelengkapan: Karena pernyataan itu benar, peribahasa yang jujur ​​meyakinkan pemeriksa yang jujur. Kelancaran: Jika pepatah tidak jujur, mereka tidak dapat membodohi pemverifikasi karena tes dilakukan beberapa kali. Akhirnya, keberuntungan pepatah harus habis. Pengetahuan Nol: Verifier tidak pernah tahu apa kata sandinya, tetapi yakin bahwa orang yang memilikinya memilikinya. Kasus # 2 Menemukan Waldo Ingat menemukan Waldo? Tentu saja, Anda harus melihatnya di suatu tempat, baik dalam kehidupan nyata maupun online. Bagi mereka yang tidak tahu, Finding Waldo adalah permainan di mana Anda harus menemukan “Waldo” di antara lautan orang. Ini adalah game “Spot the guy” yang sederhana. Hanya untuk memberi Anda ide dasar, ini adalah permainannya: Image courtesy: Youtube (IntoConnection) Dan idenya adalah menemukan Waldo yang terlihat seperti ini: Courtesy gambar: Pinterest Tampaknya cukup mudah bukan? Temukan orang ini di antara lautan orang lain yang Anda lihat dalam permainan. Ok, jadi dari mana konsep Zero Knowledge muncul di sini? Bayangkan ada dua orang Anna dan Carl. Anna memberi tahu Carl bahwa dia tahu di mana Wally berada tetapi dia tidak ingin menunjukkan di mana tepatnya dia. Jadi, bagaimana dia bisa membuktikan kepadanya bahwa dia telah menemukan Wally tanpa menunjukkan posisi yang tepat? Ada, sebuah makalah yang menarik oleh Naor, Naor dan Reingold yang menunjukkan dua solusi Zero Knowledge untuk masalah ini. Ada “Solusi Berteknologi Menengah” dan “Solusi Berteknologi Rendah”. Mari kita bahas keduanya. Solusi Mid-Tech Alasan mengapa solusi ini adalah “mid-tech” adalah karena prover dan verifier kami memerlukan akses ke mesin fotokopi untuk membuat pekerjaan ini. Jadi begini caranya. Pertama, Anna dan Carl akan membuat fotokopi dari game aslinya. Kemudian Anna, sambil memastikan bahwa Carl tidak melihat, akan memotong Waldo dari fotokopi dan kemudian menghancurkan sisanya. Setelah itu dia dapat menunjukkan Waldo cocok untuk Carl dan membuktikan bahwa dia tahu di mana Waldo setelah semua tanpa menunjukkan lokasi tepatnya ke Carl. Ada masalah dengan solusi ini. Meskipun memenuhi kriteria “Nol Pengetahuan”, itu tidak memenuhi kriteria “Kesehatan”. Ada banyak cara yang bisa dilakukan Anna untuk menipu di sini. Dia bisa saja memotong secara acak Waldo sejak awal dan bisa menunjukkannya pada Carl tanpa benar-benar tahu di mana Waldo berada. Jadi apa solusinya? Solusi untuk ini adalah pengujian yang teliti dan cermat. Pertama, Anna dan Carl akan mengambil fotokopi permainan. Kemudian Carl akan menggambar pola khas di bagian belakang fotokopi. Setelah itu, Carl akan mengantar Anna ke sebuah ruangan di mana dia akan diisolasi dan tidak memiliki kesempatan untuk menipu apa pun. Jika Anna keluar dengan potongan Waldo, maka Carl dapat diyakinkan bahwa dia benar-benar tahu di mana Waldo tanpa mengungkapkan solusinya. Mereka dapat mengulangi percobaan ini beberapa kali dan Carl dapat membandingkan guntingan berbeda dari Waldo untuk lebih yakin tentang validitas klaim Anna. Solusi Berteknologi Rendah Solusi ini membutuhkan peralatan yang sangat mendasar. Idenya sederhana. Dapatkan karton besar, yang berukuran dua kali lipat dari gim dan potong persegi panjang kecil di atasnya. Sekarang, ketika Carl tidak melihat, Anna dapat memindahkan kardus pada permainan sedemikian rupa sehingga persegi panjang langsung di atas Waldo. Sekarang, dia dapat memberitahu Carl untuk melihat dan inilah yang akan dilihatnya: Image Courtesy: Applied Cryptography Kid oleh Naor And Reingold Jadi, sementara Carl mungkin mendapatkan ide yang sangat mendasar tentang di mana sebenarnya Waldo berada, dia tidak tahu lokasi yang tepat. Karenanya Anna telah membuktikan kepada Carl bahwa dia tahu di mana Waldo tanpa menentukan lokasi pastinya. Kasus # 3: Sudoku Aplikasi hebat lain dari pengetahuan nol adalah di Sudoku. Bagi mereka yang tidak tahu, Sudoku adalah teka-teki Jepang di mana Anda mendapatkan meja 9X9 yang terlihat seperti ini: Gambar milik: Blog Kompleksitas Komputasi. Idenya adalah untuk mengisi setiap baris, setiap kolom dan setiap blok 3X3 dengan angka 1-9 dan tidak ada angka yang harus diulang. Jadi, solusi untuk teka-teki di atas terlihat seperti ini: Gambar milik: Blog Kompleksitas Komputasi. Seperti yang Anda lihat, setiap baris, kolom, dan blok 3X3 unik dan tidak ada satu nomor pun yang diulang. Mari kita kembali ke teman lama kita Anna dan Carl. Anna telah menemukan solusi untuk teka-teki Sudoku dan Carl, skeptis bahwa dia tidak percaya padanya dan ingin Anna membuktikan bahwa dia memang tahu solusinya. Anna ingin membuktikan kejujurannya, tetapi pada saat yang sama, dia tidak ingin Carl tahu solusi pasti dari teka-teki itu. Bagaimana dia melakukannya? Anna akan menggunakan Zero Knowledge untuk membuktikan validitas klaimnya. Pertama, Carl akan menjalankan solusi Sudoku melalui program komputer yang telah diverifikasi, jujur ​​dan program akan menjalankan angka-angka melalui cipher substitusi yang dipilih secara acak. Katakanlah, untuk masalah khusus ini sandi yang telah dipilih program adalah ini: Program dan sandi yang dipilih sedemikian rupa sehingga setiap digit memiliki peluang yang sama untuk ditransmutasikan ke dalam substitusi seperti halnya angka lainnya. Pada dasarnya, 1 memiliki peluang yang sama untuk ditransmisikan seperti halnya 3 dan 4 memiliki peluang yang sama untuk ditransmutasikan menjadi 9 dan seterusnya dan seterusnya. Jadi, menggunakan cipher ini memberi kita solusi berikut untuk teka-teki di atas: Gambar courtesy: Computational Complexity Blog. Anna mendapatkan solusi yang ditransmisikan sekarang, perlu diingat bahwa Carl masih tidak tahu apa solusi aslinya dan dia juga tidak memiliki solusi yang ditransmisikan. Jadi, yang dilakukan Anna sekarang adalah dia menyembunyikan semua angka dalam teka-teki dengan menggunakan “mekanisme kotak kunci”, pada dasarnya Carl tidak akan dapat melihat angka-angka itu dan akan melihat kisi kosong 9X9 di depannya. Carl sekarang memiliki 28 pilihan di depannya: Ungkapkan satu baris. Buka kolom. Buka kotak 3X3. Mengungkapkan versi transmutasi dari teka-teki asli. Misalkan Carl ingin tahu seperti apa baris ketiga: Image courtesy: Blog Kompleksitas Komputasi. Ini yang akan dia lihat. Carl akan melihat bahwa setiap angka di baris itu unik dan karena setiap angka yang mungkin dalam solusi asli memiliki probabilitas yang sama untuk ditransmisikan melalui cipher, Carl tidak akan tahu apa solusi aslinya. Sekarang anggaplah, Carl memutuskan untuk mengambil opsi terakhir dan ingin melihat seperti apa teka-teki aslinya ketika ditransmisikan: Gambar courtesy: Computational Complexity Blog. Sekali lagi, karena sandi dipilih secara acak dan semua angka memiliki probabilitas yang sama untuk ditransmisikan, Carl tidak akan tahu apa solusi aslinya. Carl sekarang bisa melalui semua 28 pilihannya dan akhirnya dia akan puas dengan validitas pernyataan Anna. Mengapa? Karena, jika Anna memang selingkuh, tidak mungkin dia bisa menemukan sandi untuk memberikan solusi unik untuk semua 28 pilihan Carl. Jika Carl hanya memilih satu opsi, peluang Anna lolos dari kecurangan adalah 27/28. TETAPI jika Carl memilih untuk melakukan tes acak beberapa kali, misalkan dia memilih untuk mengujinya 150 kali, pilihan Anna untuk lolos dengan kecurangan turun ke (27/28) ^ 150 yang <0,5%. Jadi, mari kita periksa nol properti pengetahuan dari skenario ini: Kelengkapan: Program sandi yang digunakan telah diverifikasi, jujur, dan baik Anna maupun Carl mengikuti protokol. Kesehatan: Jika Carl melakukan tes acak 150 kali, peluang Anna lolos dari kecurangan adalah <0,5%. Zero-Knowledge: Anna tidak pernah mengungkapkan kepada Carl apa solusi aslinya. Proof vs Proof Of Statement Sekarang kita tahu aspek teoritis dari nol bukti pengetahuan dan penerapannya dalam berbagai contoh, apa aplikasi praktisnya di blockchain? Mengapa semua orang mengoceh tentang Zcash untuk menerapkan ZKP (tanpa bukti pengetahuan) dan mengapa semua orang senang dengan Ethereum melakukan hal yang sama? Sebelum kita membahasnya, penting untuk mengetahui satu lagi konsep teoretis yang penting. Apa sebenarnya yang kita buktikan dengan menggunakan ZKP? Dalam spektrum luas, ada dua pernyataan yang bisa Anda buktikan dengan menggunakan ZKP. Bukti alias fakta dan bukti pengetahuan. Bukti: Ini adalah kebenaran intrinsik tentang alam semesta yang mungkin ingin Anda buktikan melalui ZKP. Misalnya. “Nomor X milik grup Y”. Bukti pengetahuan: Anda mungkin juga ingin membuktikan bahwa Anda memiliki pengetahuan tentang ide tertentu tanpa mengungkapkan apa itu pengetahuan tertentu. Seperti dapat dilihat pada contoh gua Sudoku, Waldo dan Alibaba yang diberikan di atas. Penting untuk dicatat perbedaan antara keduanya karena mereka sama sekali berbeda. Dalam dunia cryptocurrency, kita sebagian besar fokus pada “bukti pengetahuan”. Salah satu terobosan paling penting dalam membuktikan bukti pengetahuan melalui nol bukti pengetahuan datang ketika Claus-Peter Schnorr pada 1980-an muncul dengan protokol identifikasi Schnorr. Protokol ini memberikan dasar-dasar kriptografi tanda tangan kunci modern dan menampilkan bagaimana Zero-knowledge dapat diintegrasikan dengan mulus ke dalam praktik kriptografi modern. Protokol Identifikasi Schnorr Untuk memahami apa itu Identifikasi Schnorr, mari kita kembalikan teman lama kita Anna dan Carl. Anna telah mengumumkan kepada dunia bahwa dia memiliki kunci publik dan dapat menerima dan menerima informasi melalui itu. Carl, yang selalu skeptis, berpikir bahwa Anna berbohong. Satu-satunya cara Anna dapat membuktikan kejujurannya adalah dengan menunjukkan kunci pribadinya kepada Carl, tetapi ia tidak ingin mengungkapkan kunci pribadinya. Jadi, bagaimana Anna akan mengungkapkan pengetahuannya tentang kunci pribadinya tanpa mengungkapkannya? Di sinilah protokol Schnorr masuk. Bahkan sebelum kita mulai memahami cara kerja protokol, ada beberapa parameter yang perlu Anda ketahui: p = Semua bilangan prima. q = faktor p-1. “A” sedemikian rupa sehingga a ^ q = 1 mod hlm. Sekarang perlu diingat, dalam protokol Schnorr, 3 variabel ini bersifat global. Berarti siapa pun memiliki pengetahuan tentang apa 3 variabel ini untuk skenario tertentu. Sekarang kita sampai pada dua kunci, kunci privat rahasia yang akan kita sebut “s” dan kunci publik yang akan kita sebut “v”. s dapat berupa nilai apa saja selama 0 <s Satu-satunya cara Anna dapat membuktikan kejujurannya adalah dengan menunjukkan kunci pribadinya kepada Carl, tetapi ia tidak ingin mengungkapkan kunci pribadinya. Jadi, bagaimana Anna akan mengungkapkan pengetahuannya tentang kunci pribadinya tanpa mengungkapkannya? Di sinilah protokol Schnorr masuk. Bahkan sebelum kita mulai memahami cara kerja protokol, ada beberapa parameter yang perlu Anda ketahui: p = Semua bilangan prima. q = faktor p-1. “A” sedemikian rupa sehingga a ^ q = 1 mod hlm. Sekarang perlu diingat, dalam protokol Schnorr, 3 variabel ini bersifat global. Berarti siapa pun memiliki pengetahuan tentang apa 3 variabel ini untuk skenario tertentu. Sekarang kita sampai pada dua kunci, kunci privat rahasia yang akan kita sebut “s” dan kunci publik yang akan kita sebut “v”. s dapat berupa nilai apa saja selama 0 <s Satu-satunya cara Anna dapat membuktikan kejujurannya adalah dengan menunjukkan kunci pribadinya kepada Carl, tetapi ia tidak ingin mengungkapkan kunci pribadinya. Jadi, bagaimana Anna akan mengungkapkan pengetahuannya tentang kunci pribadinya tanpa mengungkapkannya? Di sinilah protokol Schnorr masuk. Bahkan sebelum kita mulai memahami cara kerja protokol, ada beberapa parameter yang perlu Anda ketahui: p = Semua bilangan prima. q = faktor p-1. “A” sedemikian rupa sehingga a ^ q = 1 mod hlm. Sekarang perlu diingat, dalam protokol Schnorr, 3 variabel ini bersifat global. Berarti siapa pun memiliki pengetahuan tentang apa 3 variabel ini untuk skenario tertentu. Sekarang kita sampai pada dua kunci, kunci privat rahasia yang akan kita sebut “s” dan kunci publik yang akan kita sebut “v”. s dapat berupa nilai apa saja selama 0 <s tapi dia tidak mau mengungkapkan kunci pribadinya. Jadi, bagaimana Anna akan mengungkapkan pengetahuannya tentang kunci pribadinya tanpa mengungkapkannya? Di sinilah protokol Schnorr masuk. Bahkan sebelum kita mulai memahami cara kerja protokol, ada beberapa parameter yang perlu Anda ketahui: p = Semua bilangan prima. q = faktor p-1. “A” sedemikian rupa sehingga a ^ q = 1 mod hlm. Sekarang perlu diingat, dalam protokol Schnorr, 3 variabel ini bersifat global. Berarti siapa pun memiliki pengetahuan tentang apa 3 variabel ini untuk skenario tertentu. Sekarang kita sampai pada dua kunci, kunci privat rahasia yang akan kita sebut “s” dan kunci publik yang akan kita sebut “v”. s dapat berupa nilai apa saja selama 0 <s tapi dia tidak mau mengungkapkan kunci pribadinya. Jadi, bagaimana Anna akan mengungkapkan pengetahuannya tentang kunci pribadinya tanpa mengungkapkannya? Di sinilah protokol Schnorr masuk. Bahkan sebelum kita mulai memahami cara kerja protokol, ada beberapa parameter yang perlu Anda ketahui: p = Semua bilangan prima. q = faktor p-1. “A” sedemikian rupa sehingga a ^ q = 1 mod hlm. Sekarang perlu diingat, dalam protokol Schnorr, 3 variabel ini bersifat global. Berarti siapa pun memiliki pengetahuan tentang apa 3 variabel ini untuk skenario tertentu. Sekarang kita sampai pada dua kunci, kunci privat rahasia yang akan kita sebut “s” dan kunci publik yang akan kita sebut “v”. s dapat berupa nilai apa saja selama 0 <s Bahkan sebelum kita mulai memahami cara kerja protokol, ada beberapa parameter yang perlu Anda ketahui: p = Semua bilangan prima. q = faktor p-1. “A” sedemikian rupa sehingga a ^ q = 1 mod hlm. Sekarang perlu diingat, dalam protokol Schnorr, 3 variabel ini bersifat global. Berarti siapa pun memiliki pengetahuan tentang apa 3 variabel ini untuk skenario tertentu. Sekarang kita sampai pada dua kunci, kunci privat rahasia yang akan kita sebut “s” dan kunci publik yang akan kita sebut “v”. s dapat berupa nilai apa saja selama 0 <s Bahkan sebelum kita mulai memahami cara kerja protokol, ada beberapa parameter yang perlu Anda ketahui: p = Semua bilangan prima. q = faktor p-1. “A” sedemikian rupa sehingga a ^ q = 1 mod hlm. Sekarang perlu diingat, dalam protokol Schnorr, 3 variabel ini bersifat global. Berarti siapa pun memiliki pengetahuan tentang apa 3 variabel ini untuk skenario tertentu. Sekarang kita sampai pada dua kunci, kunci privat rahasia yang akan kita sebut “s” dan kunci publik yang akan kita sebut “v”. s dapat berupa nilai apa saja selama 0 <s kunci pribadi rahasia yang akan kita sebut “s” dan kunci publik yang akan kita sebut “v”. s dapat berupa nilai apa saja selama 0 <s kunci pribadi rahasia yang akan kita sebut “s” dan kunci publik yang akan kita sebut “v”. s dapat berupa nilai apa saja selama 0 <s